円錐曲線(二次曲線)の群構造の作図
#数楽 円の群構造。円上の点Oを固定。円上の点A,Bに対して直線ABと平行な点Oを通る直線と円の他の交点がA+B。Ω+Ω=O。A,B,-(A+B)は点Oの接線と直線OΩに平行な漸近線を持つ双曲線でΩを通るものとの他の3交点。https://www.geogebra.org/m/xbrMSVt5
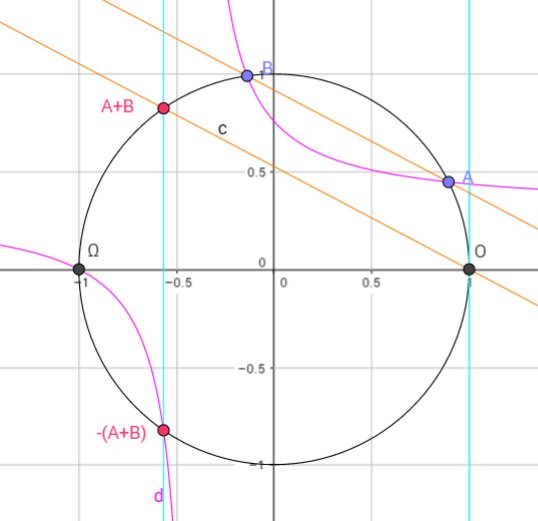
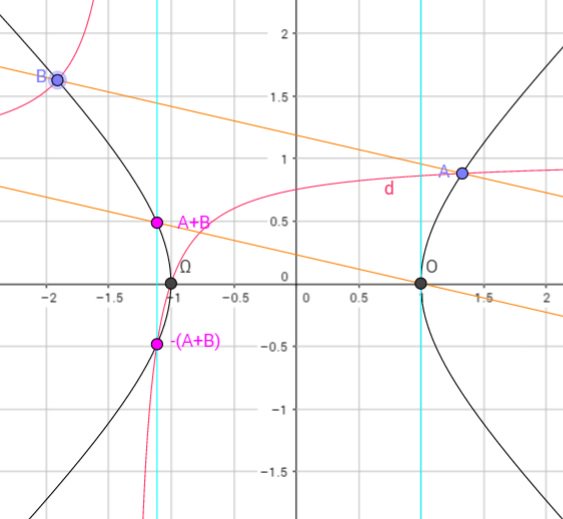
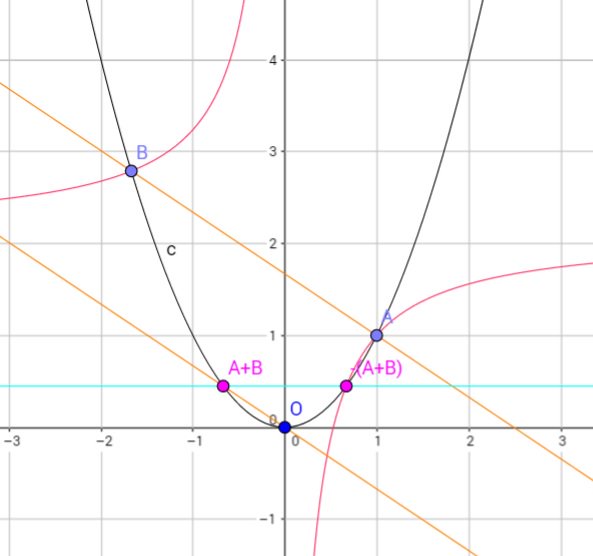
#数楽 放物線の構造。双曲線の漸近線はy軸とx軸に平行な直線。https://www.geogebra.org/m/eqJerCxh pic.twitter.com/wUgTFs8C1z
#数楽 円錐曲線の群構造を平行な二直線で定義することは分かり易くてかつ計算も易しい。双曲線を使う別の同値な群構造の定義は、計算は複雑になるが、楕円曲線のEdwards標準形の場合にそのまま同形式で一般化される。
#数楽 放物線のケースでは、群構造を与える双曲線の漸近線は「y軸」と「x軸に平行な直線」。言葉による説明より図を見た方がわかりやすいかも。https://twitter.com/genkuroki/status/856848787913883649 …
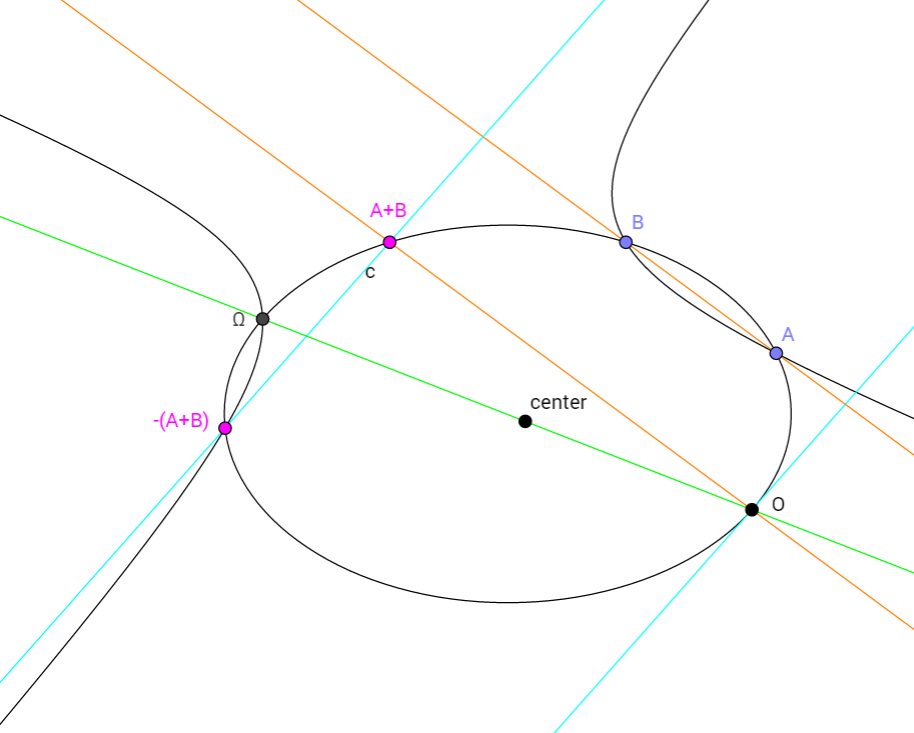
#数楽 楕円の群構造0.01https://www.geogebra.org/m/P6MpBarH 双曲線の作図は近似的無限遠にあるべき双曲線上の2点を「十分遠くの点」に取ってある。他も同様。pic.twitter.com/GEaRNZQTqU
#数楽 作図の手順楕円を描く→楕円上の任意の場所に点Oを固定→楕円上の反対側の点Ω→楕円上に2点A,B→直線AB→点Oを通る直線ABに平行な直線→それとの楕円のもうひとつの交点がA+Bの定義→続く
#数楽 →楕円の点Oでの接線→点A+Bを通るそれに平行な直線→それと楕円のもうひとつの交点が-(A+B)の定義→3点Ω,A,Bを通り、漸近線が「点Oでの接線に平行な直線」と「直線OΩに平行な直線」になる双曲線を描く→それと楕円の4つ目の交点が-(A+B)に一致する。証明せよ!
#数楽 円と言えば「R[x,y]/(x^2+y^2-1)は整域だが、UFDではないことを示せ」は結構有名な良質な演習問題。C[x,y]/(x^2+y^2-1)はu=x+iy,v=x-ivとおくことによってC[u,v]/(uv-1)=C[u,1/u]と同一視できるので自明にUFD。
#数楽 歴史的な理由で、「楕円」(ellipse)、「楕円曲線」(elliptic curve)と全然違う曲線に似たような名前が付けられてしまっている。楕円曲線を「楕円曲線」と呼ぶようになった経緯は面白いが、数学の中身の理解には役に立たない。何をどう呼ぶかは数学の本質と関係ない。
#数楽 楕円は二次曲線でx^2/a^2+y^2/b^2=1という表示を持つ。楕円曲線にはy^2=x^3+ax+by^2=(1-x^2)(1-k^2x^2)x^2+y^2=1+k^2x^2y^2x^3+y^3+1=3axyなどたくさんの表示がある。
#数楽 楕円曲線の様々な表示については http://dergipark.gov.tr/download/article-file/147976 … というサーベイ論文があって非常に便利です。楕円曲線暗号への応用のために楕円曲線の群構造の具体的表示に関する詳細な研究がある。座標不変な概念にどっぷりはまりすぎている人はたまに息抜きするべき。
#数楽 リンクメモ「円錐曲線(二次曲線)は今でも十分に楽しいよ!」という論文https://arxiv.org/abs/math/0311306 …Pell conicsでのBSD予想の類似などについて。
#数楽 二次曲線だけではなく、Edwards曲線の加法公式の作図も見たい人がいると思うので投稿します(次のツイート)。b≠0の場合は捻られたEdeards曲線と呼ばれることが多いようです。私はその場合を含んでいるか否かに頓着せずに単にEdwards曲線と呼んでいます。
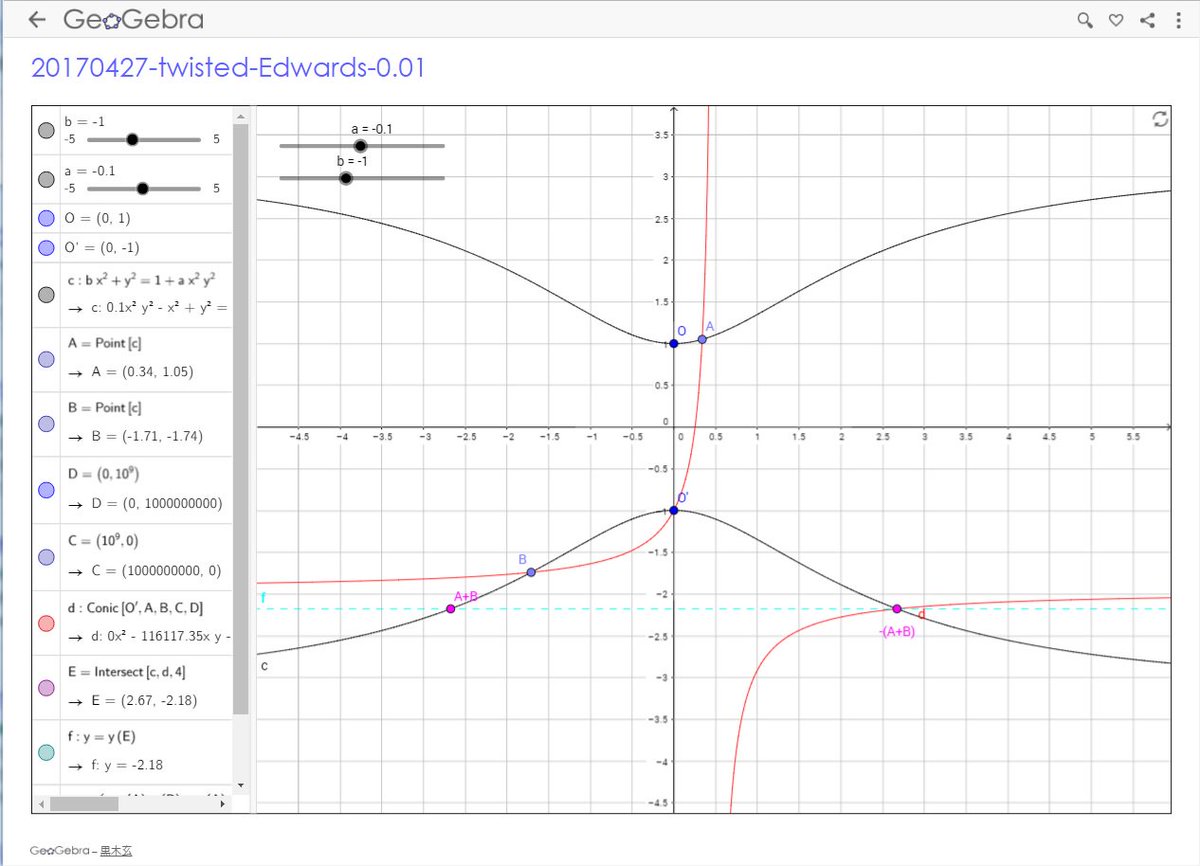
#数楽 twisted Edwards 曲線の加法公式の作図 0.01https://www.geogebra.org/m/V3DbvDqC a=0とすれば二次曲線の場合が再現されます。b=-1,a=-121665/121666に場合がEd25519で使われているEdwards曲線の実形です。pic.twitter.com/GeBICI095q



